Generative Adversarial Networks
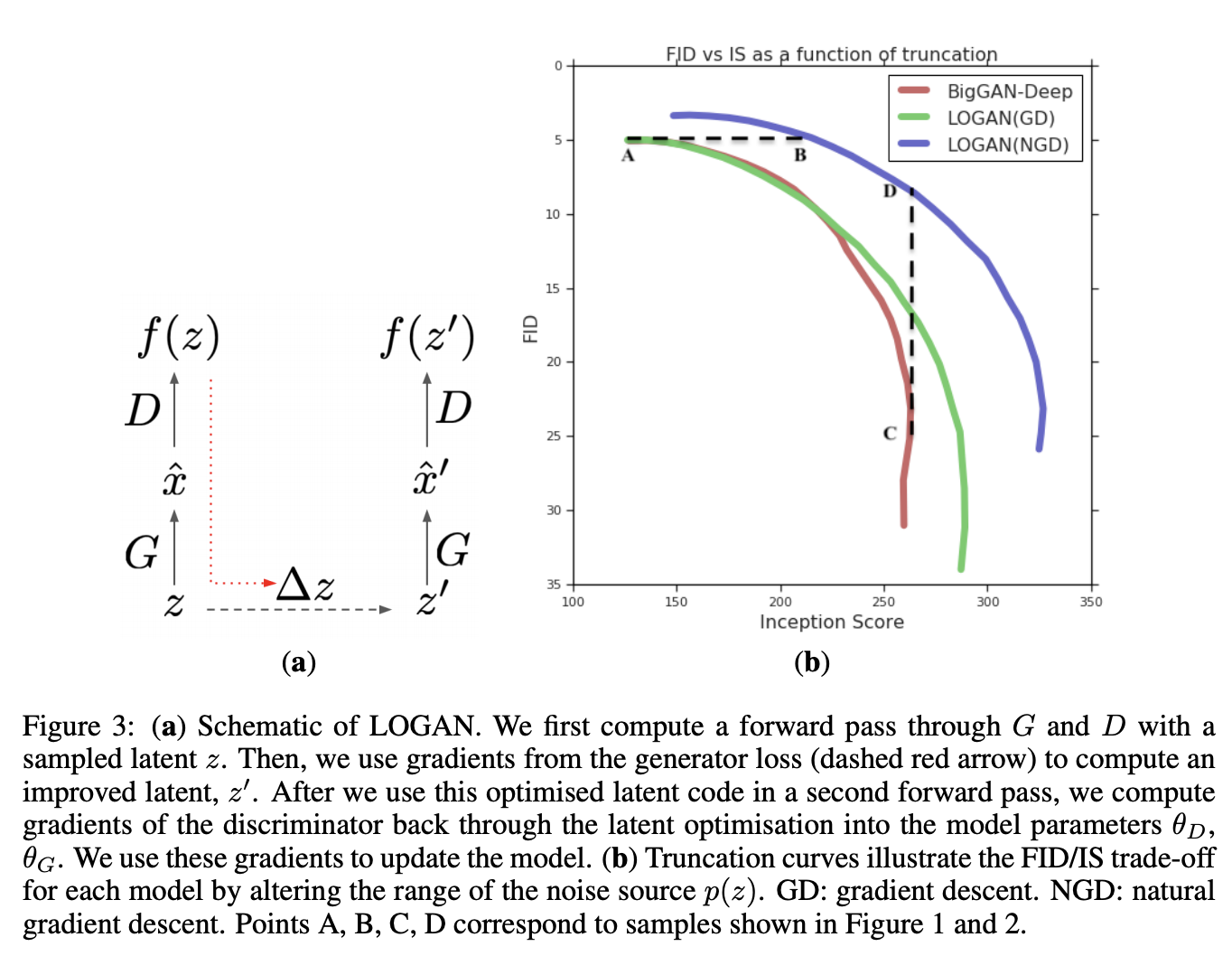
LOGAN
Introduced by Wu et al. in LOGAN: Latent Optimisation for Generative Adversarial NetworksLOGAN is a generative adversarial network that uses a latent optimization approach using natural gradient descent (NGD). For the Fisher matrix in NGD, the authors use the empirical Fisher $F'$ with Tikhonov damping:
$$ F' = g \cdot g^{T} + \beta{I} $$
They also use Euclidian Norm regularization for the optimization step.
For LOGAN's base architecture, BigGAN-deep is used with a few modifications: increasing the size of the latent source from $186$ to $256$, to compensate the randomness of the source lost when optimising $z$. 2, using the uniform distribution $U\left(−1, 1\right)$ instead of the standard normal distribution $N\left(0, 1\right)$ for $p\left(z\right)$ to be consistent with the clipping operation, using leaky ReLU (with the slope of 0.2 for the negative part) instead of ReLU as the non-linearity for smoother gradient flow for $\frac{\delta{f}\left(z\right)}{\delta{z}}$ .
Source: LOGAN: Latent Optimisation for Generative Adversarial Networks
Papers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Bias Detection | 2 | 28.57% |
| Fairness | 1 | 14.29% |
| Denoising | 1 | 14.29% |
| BIG-bench Machine Learning | 1 | 14.29% |
| Conditional Image Generation | 1 | 14.29% |
| Image Generation | 1 | 14.29% |
BigGAN-deep
Euclidean Norm Regularization
Latent Optimisation
Leaky ReLU
Natural Gradient Descent
