Single Pass PCA of Matrix Products
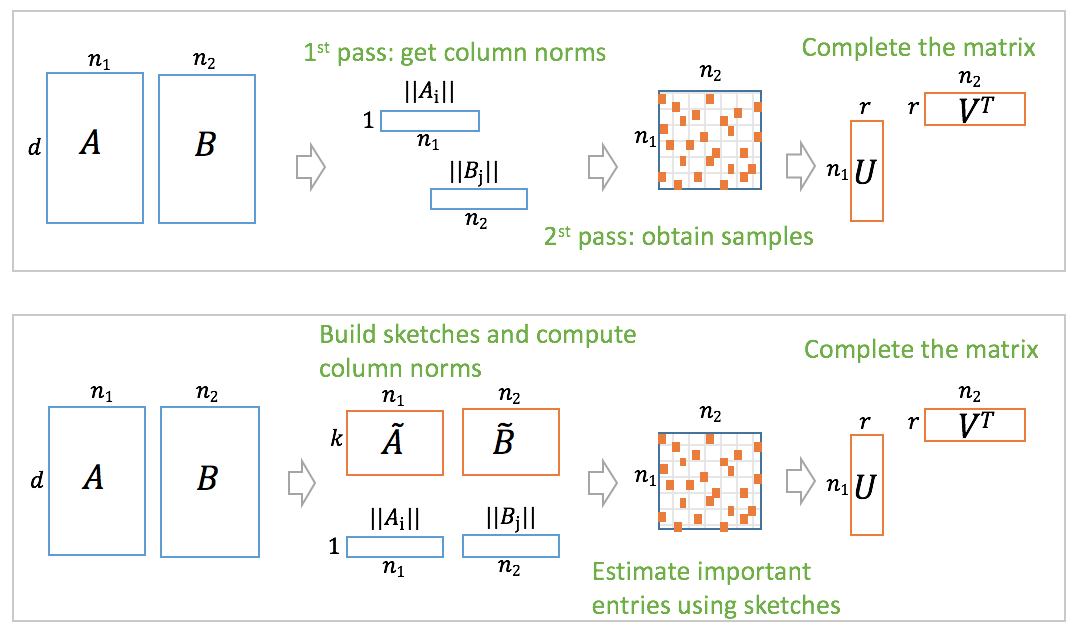
In this paper we present a new algorithm for computing a low rank approximation of the product $A^TB$ by taking only a single pass of the two matrices $A$ and $B$. The straightforward way to do this is to (a) first sketch $A$ and $B$ individually, and then (b) find the top components using PCA on the sketch. Our algorithm in contrast retains additional summary information about $A,B$ (e.g. row and column norms etc.) and uses this additional information to obtain an improved approximation from the sketches. Our main analytical result establishes a comparable spectral norm guarantee to existing two-pass methods; in addition we also provide results from an Apache Spark implementation that shows better computational and statistical performance on real-world and synthetic evaluation datasets.
PDF Abstract NeurIPS 2016 PDF NeurIPS 2016 Abstract