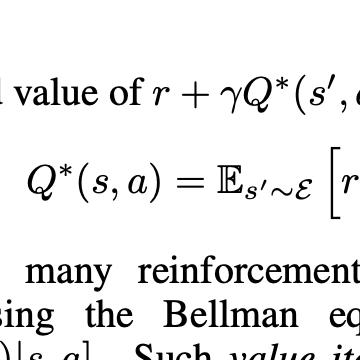Multi-step Reinforcement Learning: A Unifying Algorithm
Unifying seemingly disparate algorithmic ideas to produce better performing algorithms has been a longstanding goal in reinforcement learning. As a primary example, TD($\lambda$) elegantly unifies one-step TD prediction with Monte Carlo methods through the use of eligibility traces and the trace-decay parameter $\lambda$. Currently, there are a multitude of algorithms that can be used to perform TD control, including Sarsa, $Q$-learning, and Expected Sarsa. These methods are often studied in the one-step case, but they can be extended across multiple time steps to achieve better performance. Each of these algorithms is seemingly distinct, and no one dominates the others for all problems. In this paper, we study a new multi-step action-value algorithm called $Q(\sigma)$ which unifies and generalizes these existing algorithms, while subsuming them as special cases. A new parameter, $\sigma$, is introduced to allow the degree of sampling performed by the algorithm at each step during its backup to be continuously varied, with Sarsa existing at one extreme (full sampling), and Expected Sarsa existing at the other (pure expectation). $Q(\sigma)$ is generally applicable to both on- and off-policy learning, but in this work we focus on experiments in the on-policy case. Our results show that an intermediate value of $\sigma$, which results in a mixture of the existing algorithms, performs better than either extreme. The mixture can also be varied dynamically which can result in even greater performance.
PDF Abstract